Thermal radiative energy may be viewed as consisting of electromagnetic waves, which propagate through a medium (or through vacuum). Radiative heat transfer rates are governed by the Radiative Transfer Equation (RTE), which has six dimensions (time, space, and direction) and requires knowledge of complicated wavelength-dependent properties governed by quantum-mechanical phenomena. More detail may be found in Radiative Heat Transfer, 3rd ed.
UC Merced's Radiative Heat Transfer Laboratory has over the years carried out many experimental and theoretical investigations, although recent work has mostly concentrated on theoretical developments. Experiments were carried out to measure spectral surface properties of solids, absorption coefficients of liquids, and absorption coefficients of molecular gases; In particular, the spectral absorption coefficients of liquid glasses and the transmissivities of combustion gases were measured at high temperatures. Theoretical contributions are concentrated in three areas: development of approximate RTE solvers and of Monte Carlo methods to deal with multi-dimensional, spectral, and scattering effects; development of sophisticated spectral models for combustion gases and hypersonic plasmas (spacecraft entering an atmosphere); and modeling of turbulence-radiation interactions in combustion systems.
Some recent and current research endeavors are:
-
Determination of temperatures and concentrations from radiometric measurements in combustion systems
-
Full-spectrum k-distribution spectral models for combustion systems and nonequilibrium plasmas
-
Line-by-line spectral models for photon Monte Carlo solvers
-
Photon Monte Carlo solvers for stochastic media
-
High-order spherical harmonics RTE solvers
-
Turbulence-radiation interaction (TRI) in combustion systems
-
A general solver framework for radiative heat transfer models in combustion systems
Determination of temperatures and concentrations from radiometric measurements in combustion systems
Combustion produces high temperature combustion products, such as carbon dioxide, water vapor, carbon monoxide, etc. These gases emit and absorb electromagnetic waves in complicated way, governed by quantum mechanical energy transitions (spectral lines). The amount of emission, transmission (or absorption) of these combustion gases are uniquely related to pressure, temperature, species concentrations, etc. Therefore, temperature and concentrations can be retrieved by measuring emission or transmission in a spectrally resolved manner. Preliminary experimental setups for measuring emission or transmission of high-temperature carbon dioxide and water vapor have been constructed at UC Merced. Inverse radiation tools have been developed including: retrieving temperature and concentrations for homogeneous laminar systems from emission or transmission measurements; retrieving temperature and concentrations for nonhomogeneous laminar systems from emission measurements; retrieving mean temperature, species concentrations, their root mean square values and turbulence length scales for a homogeneous turbulent system from transmission measurements.
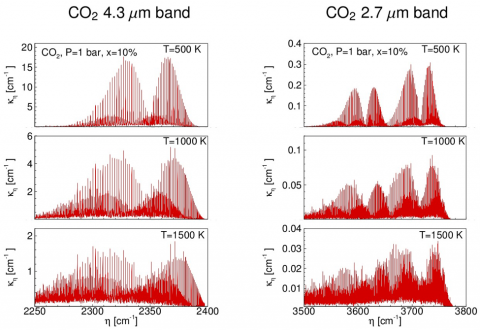
Figure 1: Two major carbon dioxide absorption bands at different temperatures.
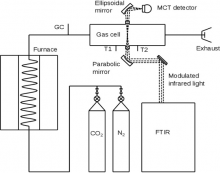
Figure 2: Experimental setup for high temperature carbon dioxide transmission measurements at UC Merced.
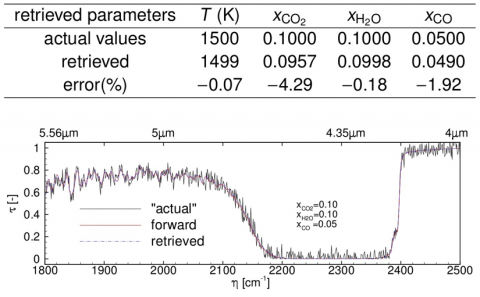
Figure 3: Inverse calculation results for retrieving temperature and species concentrations for a gas mixture from the 1800 cm−1– 2500 cm−1 spectral interval. “Actual” transmissivities were synthesized at a given temperature T=1500 K for a gas mixture containing 10% CO2+10% H2O+5% CO at atmospheric pressure for a 100-cm gas column. Temperature and all species concentrations were retrieved simultaneously.
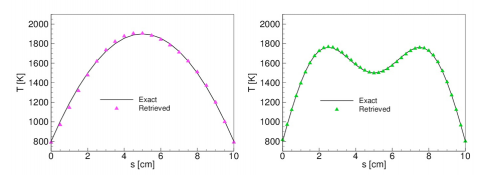
Figure 4: Comparison of retrieved temperature and exact temperature for one-peak and two-peak temperature profiles. Temperature profiles are retrieved from carbon dioxide emission measurements. Temperature profiles are retrieved from the CO2 4.3 µm band (2000 cm−1–2500 cm−1) for a 10 cm-long gas column with a uniform CO2 concentration of 20%.
Line-by-line spectral models for photon Monte Carlo solvers
Gas molecules in a combustion medium continuously emit energy in the form of photons into random directions at distinct wavenumbers, which are determined by the energy difference between the two quantized energy levels of an emitting molecule before and after emission. Photons may be absorbed or scattered by other molecules during transmission. Photon Monte Carlo (PMC) methods directly simulate such processes by releasing representative photons bundles (rays) into random directions, which are traced until they are absorbed at certain points in the medium or escape from the domain. The PMC method can deal with complicated problems, such as radiation from highly nongray combustion gases, with relative ease. Due to the rapid increase in computational power, conducting line-by-line (LBL) calculations, the most accurate radiative heat transfer simulation, has become possible. However, for nongray analysis the wavenumber carried by photon bundles must be determined in a statistically meaningful way. Line-by-line spectral models were developed with a random number-wavenumber relation database, specifically applied to PMC method. The Line-by-line spectral model, resolves all individual spectral line and is the most accurate spectral model, and maybe combined with PMC to serve as benchmark for other radiative transfer equation (RTE) solvers and spectral models. Statistically meaningful wavenumbers for the emitting photons are found from a database, which tabulating wavenumber-random number relations for each species. In order to cover most conditions found in industrial practices, the database includes a large range of pressures ranging from 0.1 bar to 80 bar, temperatures ranging from 300 K to 3000 K for CO2, H2O, CO and soot.
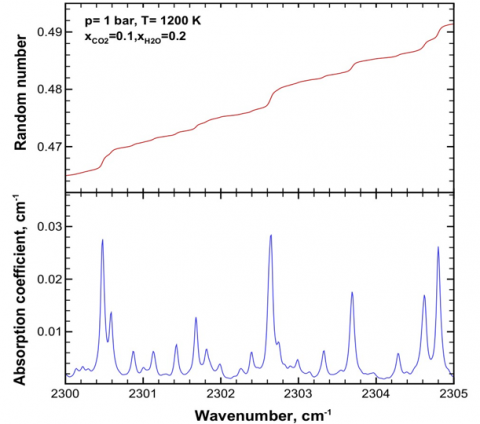
Figure 5: Random number and absorption coefficient distributions in a small spectral interval. The random number gives the probability of the number of photons emitted in a differential wavenumber interval and forms a monotonically increasing function over the whole spectrum. When a random number is drawing, the emitting wavenumber can be picked up according to this relation.
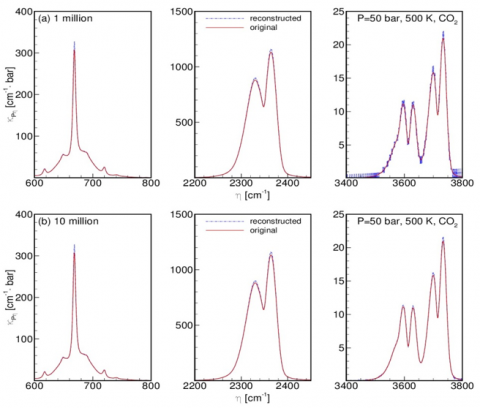
Figure 6: Reconstruction of carbon dioxide absorption coefficients from photon Monte Carlo Line-by-line spectral database by drawing different sample sizes of random numbers. The reconstructed absorption coefficients perfectly match with the original data at strong emitting spectral locations, even if only 1 million random numbers are drawn, although the reconstructed absorption coefficients fluctuate somewhat around the original data at weak emitting spectral locations. If 10 million wavenumbers are picked randomly, even absorption coefficients at weak emitting spectral locations can be reconstructed accurately.
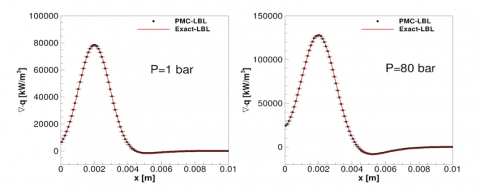
Figure 7: Comparison of calculated radiative heat sources for a nonhomogeneous mixture of carbon dioxide, water vapor, carbon monoxide and soot contained between two parallel cold black walls at atmospheric and higher pressures. With a large enough number of energy bundles, PMC-LBL results approach the exact-LBL solution with small statistical errors.
Photon Monte Carlo solvers for stochastic media
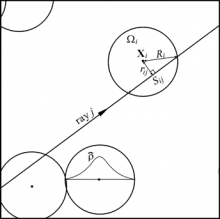
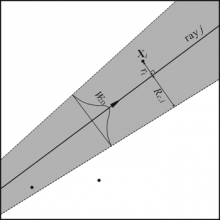
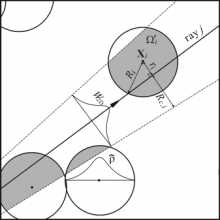
In modern turbulence research models gaseous media are increasingly modeled stochastically, i.e., the gas is represented by stochastic particles, which are point masses carrying mass, momentum, energy, etc. Similarly, actual particulate media (fuel sprays, pulverized coal) occupy tiny volume fractions, and are often modeled in Lagrangian fashion. However, traditional photon Monte Carlo methods fail for such media, since it is impossible for a train of photons (traveling along a line) to interact with point masses. Three different ray–particle interaction schemes have been devised:
[row][oneHalf]
[/oneHalf] [oneHalf]
1. Line Ray–Spherical Particle (LR-SP): the ray is model as a (traditional) volumeless line, while the point masses are assigned spherical influence regions with spherical weight function.
2. Cone Ray–Point Particle (CR-PP): the ray is assigned a small solid angle and treated as a cone, with photon energy propagating axisymmetrically in 3-D with a radially decaying weight function. Particles are point masses and can be “captured” by the cone ray.
3. Cone Ray–Spherical Particle (CR-SP): in a combination of the two interaction models the ray is modeled as a cone, while particles have spherical influence regions. The cone rays then may capture parts of the particles.
[/oneHalf][/row]
All three schemes perform about equally well, i.e., requiring roughly the same computer time and giving similar accuracy for a given number of photon bundles. Efficiency is affected by the choice of computational cell sizes, and the choice of cone opening angle (for the CR-PP and CR-SP schemes). The figure shows that the optimum cone opening angle is about 1°, giving the maximum Figure of Merit (defined as FoM = 1/2t, where is the root-mean-square relative error of the simulation and t is the simulation time).

High-order Spherical Harmonics RTE Solvers
The Radiative Transfer Equation (RTE) is an integro-differential equation with spatial and directional dependency. A deterministic solution of the RTE usually requires decoupling the spatial and angular dependency of intensity. Several approximate methods for the RTE have been developed over time, one of which is the spherical harmonics (PN) method. The Spherical harmonics method is a spectral method, which approximates the angular distribution of the intensity with a truncated series of spherical harmonics Ynm() (i.e., a two-dimensional Fourier series). The lowest order of the PN method, the P1 approximation, enjoys great popularity in both academic and industrial applications because of its simplicity (a single 2nd order PDE). However, the P1 approximation performs poorly if the intensity field has strong directional gradients, which is often the case for optically thin media. Higher-order PN methods are required to overcome this difficulty. An elliptic formulation of high-order spherical harmonics (PN) methods and the corresponding Marshak boundary conditions has been developed and applied to solve the RTE with strongly varying radiative properties. The full 3-D formulation requires solving (N–1)N/2 simultaneous elliptic PDEs, with each individual elliptic PDE efficiently solved by standard Krylov-subspace based PDE solvers, which are found in many popular CFD software packages such as FLUENT®, OpenFOAM® and Loci®.
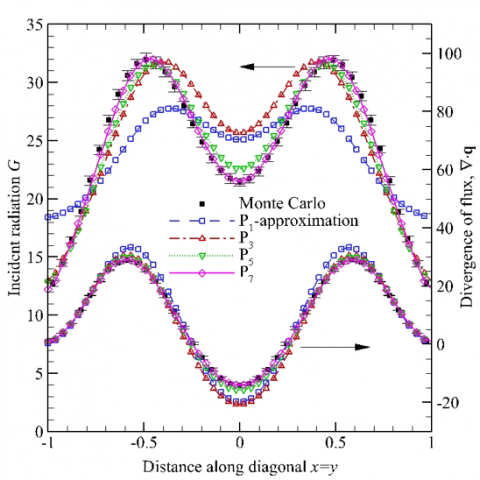
Here we show one example of the application of high-order PN methods. The radiative transfer inside a 2-D square enclosure with normalized radiative properties has been calculated using different orders of PN methods as well as the Photon Monte Carlo (PMC) method. The temperature field has an off-center peak, while the absorption coefficient decays radially from a maximum at the center. The optical thickness for this example is intermediate so that the angular distribution of the radiative intensity is fairly ballistic. The results are represented by the incident radiation and the radiative heat source, while the PMC results are taken as an accurate reference. It is seen that the prediction of the radiative heat source and incident radiation (plotted along the diagonal) gradually improves with increasing order of the PN method.

Figure 8: Spherical harmonics basis functions Ynm(q,j)
Figure 9: comparison of the performance of different levels of the PN RTE solver for a 2D gray problem.
Turbulence-radiation interactions (TRI) in combustion systems
Turbulence causes fluctuations in velocity components and composition variables (temperature and mass fractions, T, Y), which in turn cause fluctuations of the blackbody intensity Ibh(T) and the radiative absorption coefficient kh (T, Y) and, thus, intensity Ih; nonlinear interaction causes “turbulence moments” when time/ensemble-averaged.
Two strongly nonlinear turbulence correlations are required:
The first, simpler, but more important correlation is similar to the nonlinear interaction between turbulence and chemistry (TCI), and may be solved with similar tools. If a combustion system is modeled with RANS (Reynolds averaged Navier-Stokes) tools, all TCI and TRI must be modeled. If LES (large eddy simulation) is used, TCI and TRI are resolved at the filter scale, and subgrid scale effects must be modeled. In DNS (direct numerical simulations) no model is necessary. In our work we use the transported PDF method for RANS and LES calculations, in which the turbulent fluid is modeled as a large number of stochastic particles, which are traced through time and space. Radiation is modeled using a LBL PMC method developed for stochastic media, or using a conventional PN RTE solver together with the FSK spectral model.
These movies show an LES simulation of a turbulent jet flame. Starting point for all three is a quasi-steady solution without radiation; the 2nd and 3rd frames show how the flame cools down due to radiation with filter-scale resolved TRI and with fully resolved TRI, respectively (T decreases by more than 200K) .
Several general conclusions may be drawn from this work:
- Flame temperature falls 50~300 K as a result of radiative heat transfer, about 1/3-1/4 being contributed from TRI
- TRIs always enhance radiative heat transfer: Radiative heat losses are increased about 60% due to TRI
- Phenomena sensitive to temperature levels must consider TRI. For example consider production of the pollutant NO, which is lowered by more than an order of magnitude due to radiation and TRI
A general solver framework for radiative heat transfer models in combustion systems
Because of the complicated nature of thermal radiation, many radiative transfer equation (RTE) solution methods and spectral models have been proposed over the years. The objective of this work is to develop general radiative numerical tools and assemble them to provide the research community with a variety of RTE solvers and radiative property models. The developed spectral radiation calculation software (SRCS) consists of conventional deterministic RTE solvers, including Optically Thin (OT), Spherical Harmonics (PN), Discrete Ordinates (DOM), and also stochastic Photon Monte Carlo solvers. Spectral models, including gray, full spectrum k-distributions (FSK) and line-by-line (LBL) spectral models were incorporated into a spectral-model database generation package. This package is a collection of spectral-model database generation programs, which are capable of generating a pressure-based line-by-line (LBL) absorption coefficient database, a Planck-mean absorption coefficient database, full-spectrum k-distribution (FSK) look-up tables, a narrow-band (NB) FSK database, and a LBL Photon Monte Carlo (PMC) database, all from high-resolution spectroscopic databases, such as HITRAN or HITEMP.
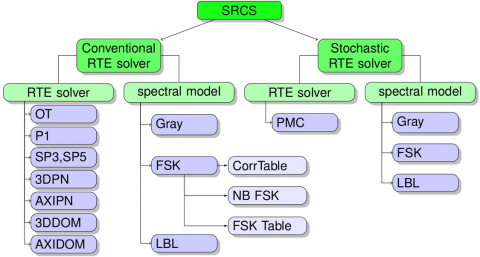
Figure 10: Structure of the spectral radiation calculation software.
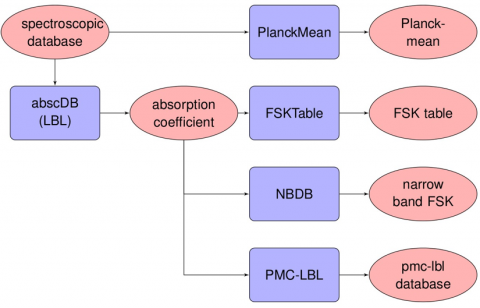
Figure 11: Structure of the spectral-model database generation package (rectangle: Fortran program, ellipse: database).
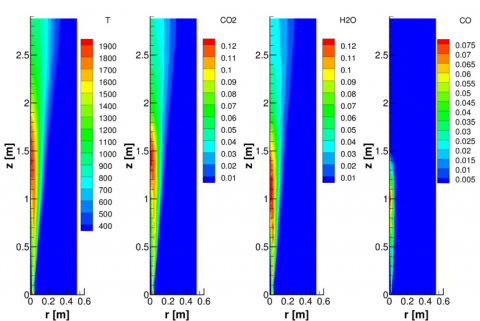
Figure 12: Time-averaged temperature and species mass fraction fields for typical turbulent jet flame.
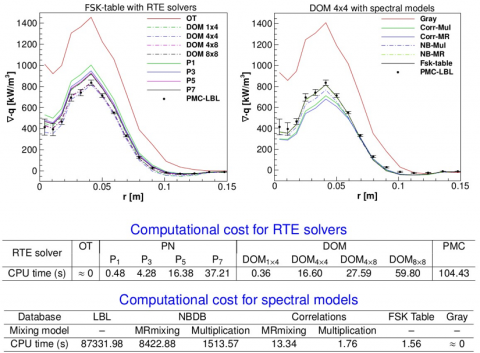
Figure 13: Accuracy and efficiency comparison for calculation of the radiative heat source in a typical turbulent jet flame, using different RTE solvers and spectral models. PMC-LBL results serve as benchmark for other RTE solvers and spectral models.
This research is being led by the Modest Group (PI: Dr. Michael Modest)